INTÉGRALES (ÉQUATIONS)

INTÉGRALES (ÉQUATIONS)

Les premières équations intégrales furent obtenues par Daniel Bernoulli vers 1730 dans l’étude des oscillations d’une corde tendue (cf. ANALYSE MATHÉMATIQUE, chap. 6). Après l’introduction du noyau de Green, il fallut attendre les dernières années du XIX^e siècle, avec les travaux de H. A. Schwarz, de H. Poincaré, de V. Volterra et surtout ceux de I. Fredholm, pour disposer de résultats généraux en liaison étroite avec les premiers développements de l’analyse fonctionnelle. Quelques années plus tard, l’étude des équations intégrales conduisait D. Hilbert à définir l’espace qui porte son nom et à poser les premières bases de la théorie spectrale, cadre dans lequel F. Riesz développa la théorie des opérateurs compacts (1918). Ainsi, les équations intégrales ont joué un rôle historique important dans l’élaboration des principaux concepts de l’analyse contemporaine.

1. Exemples

La forme usuelle d’une équation intégrale est:

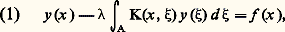où A est une partie de R^m décrite par chacune des variables x et 﨡, K une fonction donnée sur A² appelée noyau de l’équation, f une fonction donnée sur A, qui est la constante 0 dans l’équation homogène :

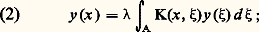enfin la fonction y est l’inconnue de l’équation et un paramètre; toutes ces quantités sont de préférence complexes.

Problème de Sturm-Liouville

Le problème de Sturm-Liouville (cf. équations DIFFÉRENTIELLES, chap. 3) concerne les valeurs du paramètre réel pour lesquelles l’équation différentielle linéaire homogène:

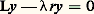(où L est un opérateur différentiel d’ordre n à coefficients continus sur un intervalle compact [a , b ] de R et r une fonction continue strictement positive sur cet intervalle) a des solutions non nulles vérifiant n conditions aux limites données.

Si 0 n’est pas l’une de ces valeurs de, on définit une fonction de Green G du problème, continue sur [a , b ]²; si l’on connaît G, la formule intégrale:

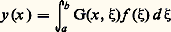donne la solution de l’équation non homogène:

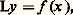vérifiant les conditions aux limites données, de sorte que le problème de Sturm-Liouville est transformé en l’équation intégrale homogène:

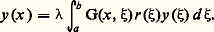Problème de Dirichlet

Le problème de Dirichlet, dans un ouvert borné de R^m , pour une fonction continue f donnée sur la frontière 臨 de , consiste à trouver la fonction, unique d’après le principe du maximum, continue sur:

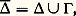harmonique sur , qui coïncide avec f sur 臨. En 1877, C. G. Neumann proposait la méthode suivante pour la solution de ce problème, en supposant m = 2 et 臨 pourvue d’une tangente continue; on désignera par L( 臨) la longueur de la courbe 臨.

Soit ( 﨡, 兀) le point courant de 臨, d’abscisse curviligne 靖, et ( 見, 廓) les cosinus directeurs de la normale en ce point orientée vers . On appelle potentiel de double couche d’une densité continue 猪 sur 臨 la limite, quand 嗀 tend vers 0, du quotient par 2 嗀 de la différence entre le potentiel de la densité 猪 au point ( 﨡 + 見嗀, 兀 + 廓嗀) et celui de la densité 漣 猪 au point ( 﨡, 兀). Le potentiel de double couche est la fonction:

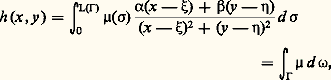où d 諸 est l’angle orienté sous lequel, du point (x , y ) 捻 , on voit l’arc d 靖 de 臨. Cette fonction est harmonique sur et, en un point (x , y ) 捻 臨, d’abscisse curviligne s , elle a pour limite:

en égalant cette limite à f (x , y ), on obtient une équation intégrale non homogène où les variables sont s et 靖, mais sans paramètre.

Henri Poincaré pressentit, dès 1896, le rôle que ce paramètre jouerait dans les résultats; cette intuition fut confirmée en 1903 par les remarquables travaux du Suédois Ivar Fredholm résumés ci-dessous (cf. chap. 3).

2. Méthode des approximations successives

Supposons A compact, le noyau K continu sur A² et, de même, f dans l’espace de Banach 暈(A) formé des fonctions y continues sur A à valeurs complexes, avec la norme:

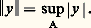Au noyau K est associé l’ opérateur intégral :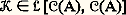

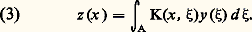qui à la fonction y 捻 暈(A) fait correspondre z = 留y 捻 暈(A) définie par:

I désignant l’application identique, on peut écrire l’équation intégrale (1):

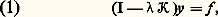et sa résolution revient à inverser l’opérateur I 漣 留; or (3) permet de déterminer la norme de l’opérateur 留:

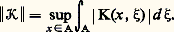Supposons maintenant || 瑩 留 瑩 麗 1. D’une part, l’équation homogène:

ne peut avoir que la solution identiquement nulle; d’autre part, la suite y ⁿ définie, à partir de y ⁰ 令 0 par exemple, par la formule de récurrence ou d’approximations successives (cf. espaces MÉTRIQUES):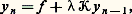

converge dans 暈(A) vers la solution de (1), à savoir:

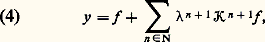留ⁿ⁺¹ étant le (n + 1)-ième itéré de l’opérateur 留, ou l’opérateur intégral associé au noyau itéré K⁽ⁿ⁺¹⁾ défini par récurrence par:

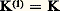et, pour n 閭 1, par:

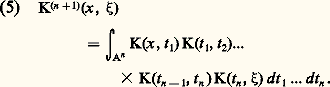On met la solution (4) sous la forme:

en introduisant l’opérateur intégral associé au noyau résolvant :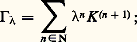

puisque (6) donne la solution unique de (1), les opérateurs I 漣 留 et I + sont inverses l’un de l’autre, d’où résulte, pour || 瑩 留 瑩 麗 1 et | 猪| 瑩 留 瑩 麗 1, la relation fondamentale entre noyaux résolvants:

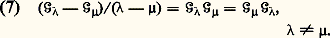Vito Volterra étudia le cas particulier A = [a , b ], a 麗 b , K(x , 﨡) = 0 pour 﨡 礪 x , K(x , 﨡) fonction continue de (x , 﨡) pour a 諒 﨡 諒 x 諒 b . Dans ce cas, l’équation (1) s’écrit:

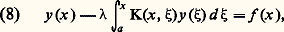et la définition (5) des noyaux itérés entraîne:

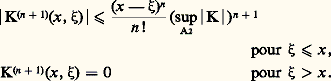C’est donc pour tout 捻 C, et non plus seulement pour || 瑩 留 瑩 麗 1 comme dans le cas général, que, d’une part, l’équation homogène n’a que la solution identiquement nulle, puisqu’elle entraîne y =ⁿ 留ⁿ y pour tout n ; que, d’autre part, la série (4) converge dans 暈(A) vers la solution de (8); enfin, on a la relation (7) quels que soient et 猪.

Les difficultés que présente le cas général furent surmontées par les deux mémoires de Fredholm de 1901 et de 1903.

3. Méthode de Fredholm

Supposons toujours A compact et le noyau K continu sur A². Si l’on partage A en p parties Aⁱ de mesures 見ⁱ , i = 1, ..., p , et si l’on choisit x ⁱ 捻 Aⁱ pour chaque indice i , on peut considérer le système linéaire:

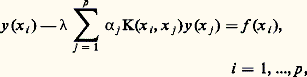comme une approximation de (1); or son déterminant est un polynôme en de degré 諒 p , dont le terme de degré n , 1 諒 n 諒 p , a pour limite, quand le plus grand des diamètres des 見ⁱ , tend vers 0, le monôme:

où la notation de Fredholm:

désigne le déterminant des n ² fonctions K(x ⁱ , 﨡^j ), i et j = 1, ..., n .

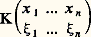Le monôme (9) est le terme général d’une série entière convergente pour tout 捻 C; en ajoutant à la série un terme constant égal à 1, on obtient une fonction entière D() appelée déterminante du noyau K et aussi déterminante du noyau transposé K 黎 défini par:

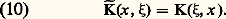Le produit de cette déterminante et du noyau résolvant est encore une fonction entière de:

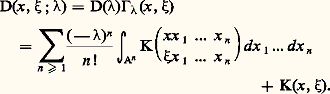Le premier théorème de Fredholm affirme que, si D() 0, pour tout second membre f 捻 暈(A), l’équation (1) a une solution unique, encore donnée par (6), avec maintenant:

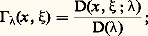c’est donc une fonction méromorphe du paramètre, et l’on a la relation (7) quels que soient et 猪.

Si au contraire est valeur singulière du noyau K, c’est-à-dire D() = 0, le deuxième théorème de Fredholm affirme que chacune des équations homogènes (2) et:

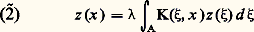a des solutions formant un espace vectoriel de dimension finie d () 礪 0 commune aux deux équations et au plus égale à l’ordre de multiplicité de la racine de la déterminante.

Si y est solution de (1) et z solution de (2), on a:

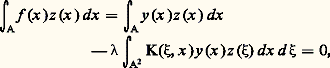d’où d () conditions linéaires que le second membre f de (1) doit vérifier pour que (1) ait une solution; le troisième théorème de Fredholm affirme que ces d () conditions nécessaires sont aussi suffisantes.

De ces trois théorèmes se dégage l’ alternative de Fredholm :

1. Ou bien l’opérateur I 漣 留 est inversible dans 硫[ 暈(A), face=F0021 暈(A)];

2. Ou bien l’opérateur I 漣 留 n’est ni injectif ni surjectif, son noyau étant de dimension finie, son image étant fermée et de codimension finie.

Le deuxième cas se présente pour les valeurs de qui annulent la déterminante: si donc il y en a, elles sont en nombre fini ou forment une suite^m秊, chaque éventualité pouvant se présenter.

4. Principaux cas particuliers

Dans le cas de Volterra (cf. supra , fin du chap. 2), la déterminante ne peut s’annuler. On retrouve ce fait en remarquant que: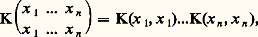

si x ¹, ..., x ⁿ sont deux à deux distincts, d’où:

Le cas de Goursat est celui où le noyau K est de la forme:

les h ⁱ étant linéairement indépendantes dans 暈(A), ainsi que les k ⁱ . Dans ce cas, on a:

pour n 礪 p ; dont D() est un polynôme de degré 諒 p et le noyau K a au plus p valeurs singulières.

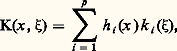
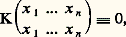Le noyau K est dit hermitien si:

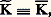c’est-à-dire si:

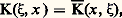quels que soient x et 﨡 捻 A. Dans ce cas, chaque déterminant de Fredholm:

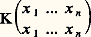est réel et les valeurs singulières aussi; car:

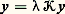entraîne la relation:

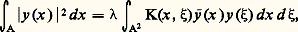où les deux intégrales sont réelles. Le noyau K a certainement au moins une valeur singulière s’il n’est pas identiquement nul, et il a certainement une suite^m , m 捻 N, de telles valeurs singulières, si le noyau n’est pas un noyau de Goursat. Le cas particulier de Goursat étant exclu, on a les formules:

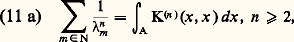et: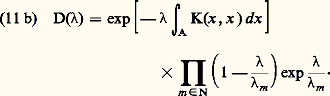

La richesse et la précision des résultats obtenus dans cette théorie, pour des noyaux quelconques et plus encore pour des noyaux hermitiens, ne sont pas seulement admirables par elles-mêmes: elles ont contribué largement à l’essor, au XX^e siècle, de l’analyse fonctionnelle en général, à l’essor de la théorie des opérateurs linéaires et à celui de la théorie des espaces préhilbertiens ou hilbertiens en particulier.

5. Opérateurs compacts

Propriété de compacité

L’inégalité de Schwarz, appliquée à (3), donne:

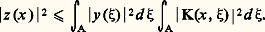et: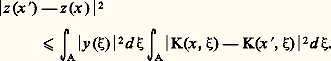

Ces inégalités suggèrent les hypothèses suivantes sur le noyau K: l’espace 硫²(A) contient chaque fonction:

et l’application xK^x est une application continue de A dans 硫²(A).

Sous ces hypothèses, réalisées en particulier si K est continu sur le compact A², que l’on munisse 暈(A) de la norme: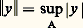

comme aux chapitres 2 et 3, ou que l’on munisse 暈(A) de la norme:

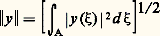définissant une topologie strictement moins fine, l’opérateur intégral 留 a cette propriété (obtenue en appliquant le théorème d’Ascoli à la suite bornée équicontinue 留y ⁿ ) que, pour toute suite y ⁿ bornée dans 暈(A), la suite 留y ⁿ contient une suite partielle convergente dans 暈(A).

Cette propriété de l’opérateur 留 fut dégagée, puis étudiée dans un espace vectoriel normé quelconque E, par le Hongrois Frédéric Riesz, sous le nom de complète continuité , auquel on préfère aujourd’hui celui de compacité : elle entraîne en effet la continuité de l’opérateur, mais s’oppose à ce qu’il ait un inverse continu, du moins si E est de dimension infinie.

La seconde norme sur 暈(A) indiquée ci-dessus a sur la première l’avantage de munir 暈(A) d’une structure préhilbertienne (cf. espace de HILBERT, chap. 1) permettant de considérer d’autre part des opérateurs auto-adjoints (cf. ci-dessous).

Valeurs spectrales

Soit E un espace vectoriel normé quelconque et 留 捻 硫(E, E): on dit qu’un nombre complexe 﨣 est valeur spectrale de 留 si l’opérateur 留 漣 﨣I n’est pas inversible dans 硫(E, E), valeur propre de 留 si 留 漣 﨣I n’est pas injectif; ceci entraîne cela, et réciproquement, si E est de dimension finie.

Soit E de dimension infinie et 留 compact: alors, la valeur 0 est spectrale, mais elle n’est pas propre en général; au contraire, si 﨣 0, on a pour l’opérateur 留 漣 﨣I l’alternative de Fredholm telle qu’elle a été énoncée à la fin du chapitre 3, de sorte qu’une valeur 﨣 0 est propre si et seulement si elle est spectrale. S’il y a de telles valeurs, elles sont en nombre fini ou forment une suite tendant vers 0.

Opérateur adjoint

Supposons désormais que la norme de E lui donne une structure préhilbertienne, donc qu’elle est associée à un produit scalaire, noté (x |y ); on dit alors que deux opérateurs 留 et 留 捻 硫(E, E) sont adjoints si:

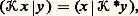quels que soient x et y 捻 E, et que 留 est auto-adjoint s’il est son propre adjoint. Ainsi, lorsque E est égal à 暈(A) muni de la seconde norme indiquée supra (cf. Propriété de compacité ), les opérateurs intégraux associés aux noyaux K et K = 力K sont adjoints.

Si 留 et 留 sont adjoints et compacts, on retrouve le troisième théorème de Fredholm sous la forme suivante: L’image de l’opérateur 留 漣 﨣I est le supplémentaire orthogonal du noyau de son adjoint 留 漣 﨣I.

Soit enfin 留 compact auto-adjoint : ses valeurs spectrales sont réelles, les noyaux de 留 漣 﨣I et 留 漣 﨣 I sont orthogonaux si 﨣 﨣 et si 瑩 留 瑩 ou 漣 瑩 留 瑩 est valeur spectrale.

Les valeurs spectrales peuvent former un ensemble fini 﨣⁰, 﨣¹, ..., 﨣ⁿ, avec 﨣⁰ = 0. Alors, le supplémentaire orthogonal du sous-espace engendré par les noyaux des:

est stable par 留 et la restriction de 留 à ce supplémentaire est un opérateur compact auto-adjoint sans autre valeur spectrale que 0, donc nul; cela veut dire que tout vecteur y 捻 E est la somme de ses projections orthogonales y ^m sur les noyaux des 留 漣 﨣^m I, m = 0, 1, ..., n , d’où les formules: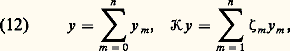

qui définissent parfaitement l’opérateur 留 et permettent, par exemple, de traiter l’équation:

où z est donné: si n’est pas valeur spectrale, l’équation a pour solution unique:

où z ^m est la projection orthogonale de z sur le noyau de:

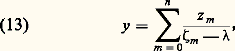
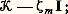si, au contraire, est une valeur spectrale 﨣 size=1^猪, l’équation n’a de solutions que si z size=1^猪 = 0; ces solutions sont encore données par (13), à ceci près que le terme de rang 猪 est remplacé par un élément quelconque du noyau de:

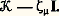Les valeurs spectrales de 留 peuvent aussi former une suite 﨣^m tendant vers 﨣⁰ = 0, et les formules (12) et (13) subsistent à condition que les séries qu’elles contiennent convergent dans E: mis à part le cas = 0, il suffit pour cela que E soit complet ou soit un espace de Hilbert. On remarque, à ce sujet, que 暈(A) n’est pas complet: pour un opérateur intégral 留 dans 暈(A), associé à un noyau K hermitien mais non noyau de Goursat, donc possédant une suite de valeurs spectrales, on a pourtant le remarquable théorème de Hilbert-Schmidt, d’après lequel la deuxième série (12) converge uniformément vers la fonction 留y .

Encyclopédie Universelle. 2012.